Pour vous aider à décortiquer le raisonnement et à trouver l’erreur, le cas échéant, voici les éléments significatifs:
- Il est établi que 1% des femmes de 40 ans auront un cancer du sein.
- Aucun test, même les meilleurs, n’est fiable à 100%. Il y a un certain nombre de cas qui ne sont pas détectés, alors que certaines femmes atteintes de la maladie reçoivent un résultat négatif. En ce qui concerne la mammographie, elle permet de détecter 80% des cancers du sein.
- Le nombre de faux positif, c’est-à-dire de mammographies positives alors qu’il n’y a pas de cancer, est de 9,6%.
Quelle est votre conclusion?
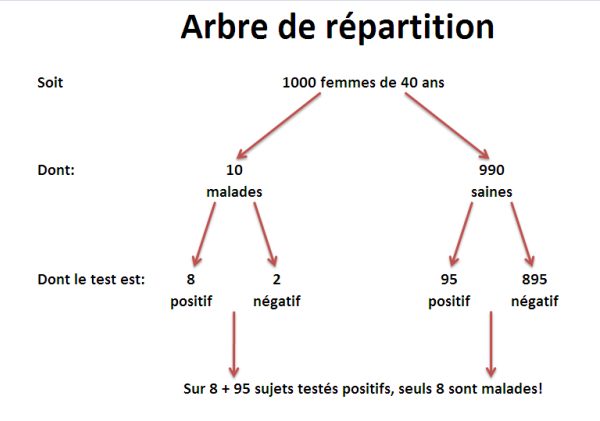
On a tendance à raisonner ainsi: sur 1000 femmes de 40 ans, 10 ont le cancer du sein (1%). 8 seront correctement diagnostiquées (80%) et pourront recevoir les soins adéquats. Cela vaut donc la peine de dépister systématiquement.
Les faux positifs
Mais que faites-vous des faux positifs? Sur ces 1000 femmes, 990 n’ont pas le cancer du sein, cependant 9,6% d’entre elles vont recevoir un diagnostic positif (erroné), ce qui ne fait pas moins de 95 personnes. En clair, on risque de pratiquer un traitement lourd et dommageable, voire ôter un sein, à 95 femmes pour en sauver 8!
Nous pouvons pousser nos calculs un peu plus loin et répondre à la question: «quelle est la proportion de femmes de 40 ans qui reçoivent un test positif ayant effectivement le cancer?» Réponse: il faut diviser le nombre de femmes ayant un cancer et diagnostiquées correctement par le nombre total des diagnostics positifs, corrects et erronés.
Pour un ensemble de 1000 femmes de 40 ans, 8 seront malades et auront un diagnostic correct et 95 ne seront pas malades mais recevront tout de même un diagnostic positif, ce qui donne.
En d’autres termes, plus de 90% des femmes de 40 ans avec un diagnostic positif n’ont en réalité pas le cancer du sein! Ainsi, aux Etats-Unis, on estime que chaque année, plus de 300 000 femmes non cancéreuses subissent une biopsie du sein.
Raisonner en fréquences naturelles
Peut-être avez-vous été perdu en cours de route? Ces calculs ne sont en effet pas simples, car très abstraits: des pourcentages n’expriment au final rien de concret (la formule mathématique exacte pour ce genre de problème, le calcul de probabilités conditionnelles, est la loi de Bayes). Il y a cependant une astuce: utilisez plutôt les fréquences naturelles, c’est-à-dire des nombres d’individus réels, et une représentation graphique en arbre de répartition.
(Voir image)
Vous avez saisi? Alors à vous de tirer les conclusions correctes du cas suivant. Quelle est la probabilité pour qu’une personne de plus de 50 ans testée positivement au dépistage du cancer colorectal (test appelé FOBT, fecal occult blood test) soit effectivement atteinte de la maladie?
Données
- Probabilité d’être atteint du cancer colorectal après 50 ans: 0,3%
- 50% de chance qu’une personne malade présente un test positif
- 3% de risque d’avoir un test positif sans être malade.
Si vous avez correctement calculé, votre résultat doit être: 4,8% (sur 15 + 299 personnes, soit 314 sujets testés positifs, seuls 15 sont effectivement malades). Etonnant, n’est-ce pas? Même des médecins aguerris s’y laissent tromper. Cela vaut donc la peine de bien considérer toutes les données d’un problème afin d’en tirer la conclusion juste. Et d’agir en conséquence…
Vous trouverez les références exactes de ces raisonnements dans l’ouvrage: Penser le risque, Apprendre à vivre avec l’incertitude, de Gerd Gigerenzer, Editions Markus Haller, 2009.